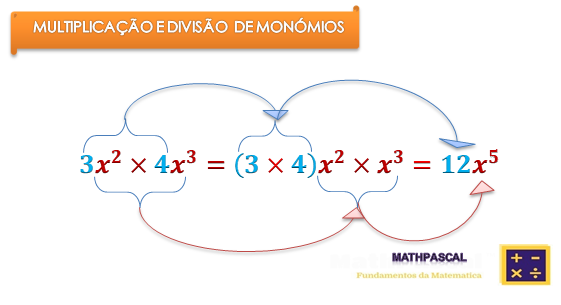
As operações da multiplicação e divisão de monómios, visa reduzir dois ou mais monómios num só, para isso devemos seguir alguns critérios.
Multiplicação de Monómios
A multiplicação de dois ou mais monómios, resulta um monómio.Então, para multiplicar dois ou mais monómios, multiplica-se os seus coeficintes e as partes literais entre si ( aplicando a propriedade da potência).
Por exemplo: Multiplique os seguintes monómios: 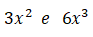
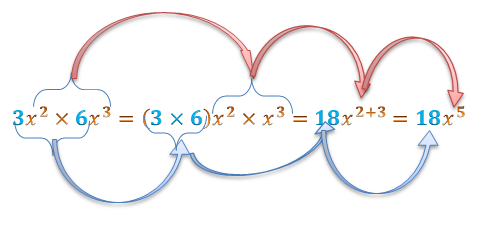
Breves explicações
- Primeiramente, multiplicou-se os coeficientes (3 x 6)=18 e as partes literais ( x^2 . x^3);
- Quanto as partes literais, aplicou-se a propridade da potência ( x^2 . x^3)=x^(2+3)=x^5;
Divisão de Monómios
Para dividir dois monómios, deve-se dividir os coeficientes entre si e as partes literais entre si( aplicando a propriedade da potência)
Por exemplo:
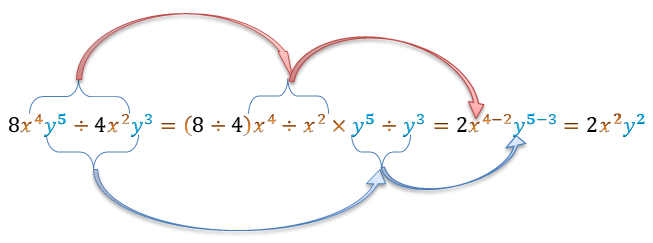
Breves explicações
- Inicialmente, dividiu-se os coeficientes entre si (8: 4)=2 e as partes literais entre si
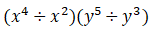
- Quanto as partes literais, aplicou-se a propriedade da pontecia do quociente de bases iguais e expontes diferentes:
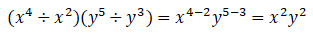
Quando os monómios estiverem na forma de fração, mantém -se a primeira fração (dividendo) e multiplica-se pelo inverso da segunda fração ( divisor).
Por exemplo:
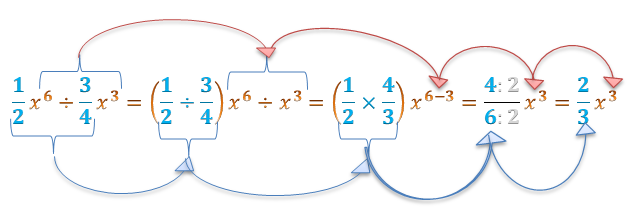
Breve Explicação
- Primeiramente, dividiu-se os coeficientes entre si (1/2 : 3/4), e as partes literais entre si (x^6 : x^3);
- Quanto aos coeficiente, manteu-se a primeira fração e multiplicou-se pelo inverso da segunda fração (1/2 x 4/3)=4/6;
- Quanto a parte literal, aplicou-se a propriedade da potência do quociente com a mesma base e expoentes diferentes (x^6 : x^3)=x^(6-3)=x^3;
Exercícios
1-Calcule a Multiplicação e Divisão de Monómios:
a)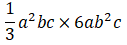
b) 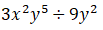
Leia também: