Ao resolver um sistema de duas equações do 1º grau a duas incógnitas aplicando a Regra de Cramer ou Método de Cramer, procura-se determinar os valores das incógnitas x e y. O método de cramer consiste em multiplicar os elementos das diagonais principais (ab1;bc1;ac1) e subtrair-lhes, respectivamente, os produtos que se obtêm multiplicando os elementos das diagonais secundárias (a1b;bc1;a1c).
Leia também:
Passos para resolver um sistema de duas equações pela regra de cramer
- Numerador é formado pelos coeficientes das incognitas;
- Denominador, obtem-se do denominador, substituindo a coluna dos coeficientes da incognita que se quer terminar, pelos termos independentes depois de transportos ao segundo menbro;
- Seguidamente, multiplicam-se os elementos das diagonais principais (ab1;bc1;ac1) e subtrair-lhes, respectivamente, os produtos que se obtêm multiplicando os elementos das diagonais secundárias (a1b;bc1;a1c).
Observação: Para facilitar nos cálculos é necessário que escreva o sistema de equação do 1º grau a duas incógnitas na forma canónica caso não esteja.
Considerando o sistema, temos:
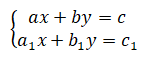
Aplicando a regra de cramer , temos a seguinte forma:
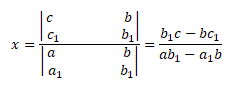
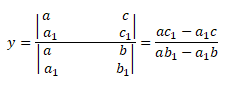
Por exemplo:
- Resolve o seguinte sistema de equações aplicando a Regra de Cramer:
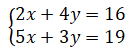
Resolução
Para resolver, o sistema de duas equações do 1º grau a duas incógnitas pelo método de cramer, primeiramente o sistema deve estar na forma canónica, posteriomente deve-se identificar os valores dos coeficiente da primeira e segunda equação. Sendo assim, temos:
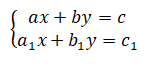
- a=2 ; b=4; c=16
- a1=5 ;b1=3 ; c1=19
Para determinar o valor x, basta subtituir os coeficientes (a=2 ;a1=5 ;b=4;b1=3 ;c=16; c1=19) na seguinte expressão abaixo:
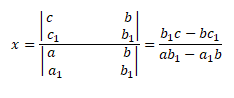
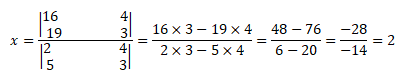
x=2
Para determinar o valor y, basta subtituir os coeficientes (a=2 ;a1=5 ;b=4;b1=3 ;c=16; c1=19) na seguinte expressão abaixo:
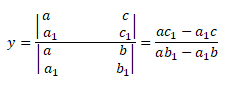
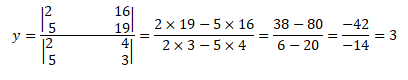
y=3
Para constatar se os valores dos pares ordenados x=2 e y=3, são solução do sistema de equação dado, basta substiuir os mesmos valores no sistema de equação.
Verificação da solução do sistema
Substitui-se, em cada equação do sistema dado: x=2 e y=31. Sendo assim, temos:
1ª equação :
- 2x+4y=16
2.2+4.3=16
4+12=16
16=16
2ª equação:
- 5x+3y=19
5.2+3.3=19
10+9=19
19=19
Obtivemos assim, um sistema equivalente ao dado, mas mais simples; a solução do sistema dado é o par de números (2;3)
Problema sobre sistema de duas equações aplicando a regra de cramer
A Mónica tem guardadas nos seus bolsos 8 guloseimas. Num deles tem o triplo das guloseimas que tem no outro. Quantas guloseimas tem em cada um?
Resolução
- Num bolso tem x gloseimas;
- No outro bolso tem y gluseimas.
x—?
y—?
Formulando as expressões, temos:
<<A Mónica tem guardadas nos seus bolsos 8 guloseimas>>. Sendo assim,temos:
x+y=8
<<Num deles tem o triplo das guloseimas que tem no outro>>. Sendo assim, temos:
x=3y
Obtem-se o sistema: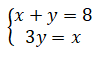
Para resolvermos o problema proposto aplicando a regra de cramer, primeiramente devemos escrever o sistema de equação na forma canónica. Sendo, assim temos:
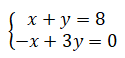
Posteriomente, devemos identificar os valores dos coeficientes das duas equações. Sendo assim, temos:
- a=1 ; b=1; c=8
- a1=-1 ;b1=3 ; c1=0
Determinando o valor da incognita x, temos:
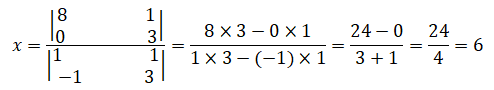
x=6
Determinando o valor da incognita y, temos:
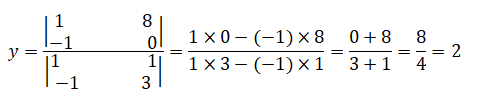
y=2
A solução do sistema dado é o par de números: (6;2).
Portanto, num bolso tem 6 goluseimas, no outro bolso tem 2 guloseimas.
Exercícios sobre a regra de cramer
1.Resolve os seguintes sistemas de equações:
- 2x+4y=2
- x-2y=1
Resolução
Para resolver, o sistema de duas equações do 1º grau a duas incógnitas pelo método de cramer, primeiramente os sistema deve estar na forma canónica, posteriomente deve-se identificar os valores dos coeficiente da primeira e segunda equação. Sendo assim, temos:
- a=2 ; b=4; c=2
- a1=1 ;b1=-2 ; c1=1
Determinando o valor de x, temos:
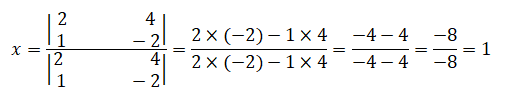
x=1
Determinando o valor de y, temos:
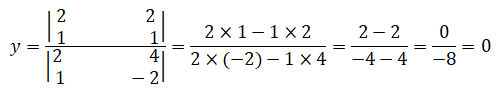
y=0
Portanto, a solução do sistema dado é o par de números: (1;0).
Leia também: