Os números surgiram da necessidade do homem contar os seus bens desde a antiguidade. Para contabilizar foi necessário a contagem. Logo esses algarismos que usamos hoje para efetuar cálculos denomina-se conjuntos dos números naturais e estão formados pelos algarismos (0,1,2,3,4,5,…), vale lembrar também que neste conjunto efetua-se algumas relações.
Ver: História dos números
Nesta aula, poderás aprender :
- Sucessor de um número natural
- Antecessor de um número natural
- Subconjuntos dos números naturais
- Domínio do conjunto dos números naturais
Posteriormente, para todos os números naturais existe sempre uma das seguintes relações: x>y, x<y ou x=y.
Relação ou comparação de números naturais
Para comparar dois ou mais algarismos usamos os seguintes símbolos: (<,>, =)
Exemplo: Compara os seguintes números:
a). 3 e 4
Para comparar estes números, primeiramente devemos analisar o os algarismos quanto as suas ordens. Neste caso, podemos dizer que 3 é menor que 4 ou 4 é maior que 3. Portanto, temos: 3<4.
b). 6 e 3
Seguidamente ao compararmos os algarismos 6 e 3 devemos analisar os números quanto as suas ordens. Logo, podemos dizer que 6 é maior que 3 ou 3 é menor que 6. Portanto, temos: 6>3.
Todos os números naturais possuem um sucessor e um antecessor.
- O sucessor de x é x+1. Logo x< x+1.
- O antecessor de x, sendo x diferente de zero é x-1. Portanto x>x-1.
Sucessor de um número natural
No conjunto dos números naturais, o sucessor é o número que vem depois dele. Para representar ou identificar o sucessor de um número basta usar a seguinte correspondência : x+1.
Por exemplo:
- O sucessor de 1 é 1+1=2. Logo o sucessor de 1 é igual a 2.
- O sucessor de 3 é 3+1=4. Logo o sucessor de 3 é igual a 4.
- O sucessor de 5 é 5+1=6. Logo o sucessor de 5 é igual a 6.
Antecessor de um número natural
No conjunto dos números naturais, o antecessor é o número que vem antes dele. Para representar ou identificar o antecessor de um número basta usar a seguinte correspondência : x-1 , sendo x diferente de zero.
Por exemplo:
- O antecessor de 7 é 7-1=6. Logo o antecessor de 7é igual a 6.
- O antecessor de 9 é 9-1=8. Logo o antecessor de 9 é igual a 8.
- O antecessor de 11 é 11-1=10. Logo o antecessor de 11 é igual a 10.
Subconjuntos dos números naturais
Existem vários subconjuntos dos números naturais. O conjunto dos números naturais representa-se pela letra N. Neste caso teremos:
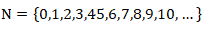
Dentro deste conjunto encontraremos o subconjunto dos números naturais não nulos. Neste caso, o número zero (0) não fara parte deste subconjunto, porque este número é nulo. Este subconjunto representa-se pela letra N*. Logo, temos:
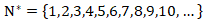
Também temos os subconjuntos dos números naturais pares, temos:
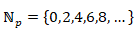
Por conseguinte, temos o subconjunto dos números naturais ímpares, temos:
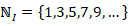
Domínio do conjunto dos números naturais
Neste conjunto de partida, abordaremos os domínios das quatro (4) operações fundamentais da matemática: Adição, subtração, multiplicação e divisão.
- Quanto a adição, apenas adiciona-se as parcelas sem nenhuma restrição;
- Posteriormente, no domínio da subtração só é possível quando o diminuendo for maior ou igual ao diminuidor. Portanto, caso a diferença é determinada univocamente ou simplesmente tem soluções quando o aditivo for maior que o subtrativo;
- Por conseguinte, neste conjunto de partida, a multiplicação efetua-se multiplicando os fatores entre si, sem nenhuma restrição;
- Neste domínio, a divisão, só é possível quando o dividendo for múltiplo do divisor, ou seja, quando dividendo for divisível pelo divisor. Logo após o quociente é determinado univocamente.
Exercícios resolvidos
- Observe os números no quadro:

a). Quais são os números naturais não negativos?
b). Quais são os números naturais?
c). Quais são os números naturais pares?
d). Quais são os números naturais impares?
e). Qual é o número natural par que não é negativo nem positivo?
Resolução
a). Observando a tabela, podemos dizer que os números naturais não negativos são: (1, 4, 9, 12, 13).
b) Analisando os valores que estão na tabela, os números naturais são: (0, 1, 4, 9, 12, 13).
c). Logo, os números naturais pares são: (4, 12).
d). Posteriormente, podemos dizer que os números naturais ímpares são: ( 1, 9, 13).
e). Quanto a tabela acima, o número natural par que não é negativo nem positivo é o algarismo zero (0).
Leia também:


