O presente plano de aula sobre fracção geratriz é fundamental, porque ajudará o docente na introdução sobre o tema e a obter tecnicas de como ensinar.
TEMA I: APROFUNDAMENTO DE ESTUDO DOS NÚMEROS E OPERAÇÕES
SUBTEMA: NÚMEROS REAIS
SUMÁRIO: FRACÇÃO GERATRIZ
- Fracção geratriz de uma dizima periodica simples
- Fracção geratriz de uma dizima periodica composta
Objectivos especificos
- Calcular a fracção geratriz de uma dizima periodica simples;
- Calcular a fracção geratriz de uma dizima periodica composta.
Sugestões Metodologicas
« Primeiramente é crucial explicar ao aluno como subtrair e multiplicar números decimais (dizimas). Seguidamente, explique o conceito da fracção geratriz de forma clara e simples, usando exemplos praticos do dia a dia para facilitar a compreensão dos alunos;
Inicie a aula mostrando aos alunos que as fracções geratrizes podem ser representadas de forma decimal, destacando a recorrencia de alagarismo e o seu periodo;
Promova a interdisciplinaridade, relacionando o tema das fracções geratrizes com outras ciencias como, a história, a geografia (…) »
Introdução
Problema:
(Geografia) Um país tem uma taxa de natalidade de ao ano. Qual é a representação dessa taxa em forma de fracção?
Resolução
Para representar essa taxa como uma dizima infinita periodica em forma de fracção, primeiro precisamos identificar o padrão de repetição( trata-se de uma dizima periodica simples). Vamos transformar em forma de fracção:
Transformando 1,666… em fracção, temos:
(1ª equação) Primeiramente, igualamos a dizima por uma incógnita (x), temos:
x=1,666…
(2ª equação) Multiplicando ambos menbros da equação por 10, temos:
x=1,666…/.(10)
10x=16,666…
Subtraindo a segunda equação na primeira equação, temos:
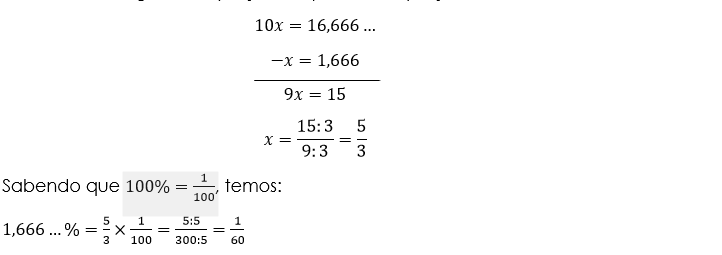
Portanto a taxa de natalidade do país é 1/60 em forma de fracção.
Fracção Geratriz
A fracção geratriz é aquela que quando dividimos seu numerador pelo denominador o resultado será sempre uma dizima periodica.
Os números decimais estão compostos por uma parte inteira e decimal. As dizimas periodicas podem ser: Dizima periodica simples e Dizima periodica composta.
- Dizima periodica simples: é quando a aparte decimal é composta apenas pelo periodo.
Por exemplo: 4/9=0,444…
- Dizima periodica composta: é quando na parte decimal existir um número ou mais que não se repetem .
Por exemplo: 52/90=0,5222…
Fracção geratriz de uma dizima periodica simples
Para escrever a fracção geratriz de uma dizima periodica simples, podemos seguir os seguintes passos:
- Igualar a dizima periodica a uma incognita, de forma a escrever uma equação do 1º grau.
- Multiplicar ambos os lados da equação por um multiplo de 10 ( Para descobrir qual será o multiplo, devemos identificar quantas casas decimais devemos andar para que o periodo fique antes da virgula).
- Diminuir a equação encontrada na equação inicial.
- Isolar a incognita.
Por exemplo: Encontre a fracção geratriz do número 0,888…
Primeiramente, igualamos a dizima por uma incógnita (x), temos:
x=0,888…
Multiplicando ambos menbros da equação por 10, temos:
x=0,888…/.(10)
10x=8,888…
Subtraindo a segunda equação na primeira equação, temos:
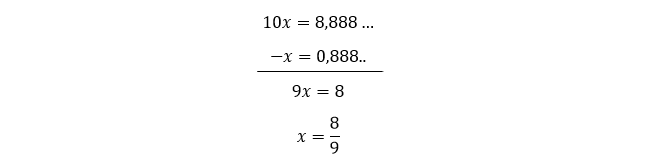
Portanto a fracção geratriz da dizima 0,888… é ou seja 8/9=0,888…
Fracção geratriz de uma dizima periodica composta
Quando a dizima periodica for composta, além dos passos indicados para simples, devemos tambem multiplicar a primeira equação por um multiplo de 10 que a transforme em uma dizima simples.
Por exemplo: encontre a fracção geratriz de 2,361616161…
(1ª equação) Igualando a dizima por uma incógnita,temos:
x=2,3616161…
(2ª equação) Multiplicamos por 10,temos:
x=2,3616161…/.(10)
10x=23,616161…
(3ª equação) Multiplicamos por 1000,temos:
x=2,3616161…/.(1000)
1000x=2361,616161…
Subtraindo 3ª equação, na 2ª equação, temos:
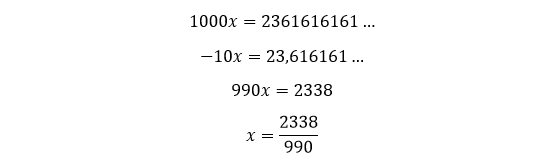
A fracção geratriz da dizima 2,36161… é 2338/990.
Exercicios de Aplicação sobre fracção geratriz
Quanto aos exercicios sobre o plano de aula sobre fracção geratriz, fará com que o aluno tenha mais conhecimento sobre o assunto.
- Uma fracção geratriz é 0,666… Qual é o valor dessa fracção?
- Se uma fracção geratriz é 0,4333…, como podemos escreve-la de forma fraccionaria?
- Um rio tem um comprimento de 0,583333…km. Qual é a sua representação em forma de fracção e em cm?
- Se uma fracção geretriz é 0,272727… qual é o valor exato dessa fracção?
- Se uma fracção geratriz é 0,23999… qual é o seu valor real?
LEIA TAMBEM:

