PROGRESSÃO ARITMÉTICA

A progressão aritmética, também conhecida como PA, é uma sequência na qual a diferença entre o sucessor e o antecessor é uma constante (r), ou seja a_n+1-a_n=r. Nesse caso, n pertence ao conjunto de números naturais e r é a razão da progressão.

Nesta aula aprenderás, sobre:

• Monotonia da PA
• Termo geral da PA
• Soma dos n termos da PA
• Exercicios sobre PA

Onde:

   r: Razão da PA

  n: Números de termos

  a_n: Primeiro termo (antecessor)

  a_n+1: Segundo termo ( sucessor)

Monotonia de uma progressão aritmética

• Quando r>o, a PA é monótona crescente;
• Quando r<o, a PA é monótona decrescente;
• Quando r=o, a PA é monótona constante;

Por exemplo: Analise se as seguintes sucessões são aritméticas. Em caso afirmativo indique a respectiva razão e analise a sua monótonia.

5; 7; 9; 11;…

Para determinar se é uma progressão aritmetica, basta calcular a razão. Sendo assim, temos:

a₁=5 ; a₂=7

Calculando a diferença entre os dois termos, temos: a₂-a₁=r

7-5=r

r=2

a₃=9 ; a₄=11

Calculando a diferença entre os dois termos, temos: a₃-a₂=r

11-9=r

r=2

Pode-se observar que a diferença da progressão é 2. Sendo assim, pode-se dizer que a progressão é aritmetica pois a diferença entre o sucessor e o antecessor é uma constante (2).

Termo geral de uma progressão aritmética(PA)

Sabendo que a_n+1-a_n=r. Para determinar o termo geral, basta calcular as seguintes expressoes:

a₂-a₁=r…a₂=a₁+r

Substituindo a₂=a₁+r na segunda progressão, temos:

a₃-a₂=r…a₃=a₂+r…a₃=a₁+r+r…a₃=a₁+2r

Substituindo a₃=a₁+2r na terceira progressão, temos:

a₄-a₃=r…a₄=a₃+r…a₄=a₁+2r+r…a₄=a₁+3r

De forma geral, observa-se que o primeiro termo mantem-se em todos os termos, enquanto que a razao vai aumentando em 1 unidade. Neste caso, temos:

a_n=a₁+(n-1)r —> Fórmula do termo geral de uma progressão aritmética.

Por exemplo: Numa PA de razão 3, sabe-se que o primeiro termo é 6. Determine o termo geral.

Dados

• r=3
• a₁=6
• a_n-?

Neste caso para determinar o termo geral, temos que substituir os dados na fórmula do termo geral, assim temos:

a_n=a₁+(n-1)r

a_n=6+(n-1).3

a_n=6+3n-3

a_n=3n+3

Portanto o termo geral da progressão aritmetica é a_n=3n+3.

Soma dos n primeiros termos de uma PA

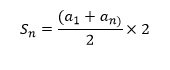
Por exemplo: Numa PA com 15 termos em que o primeiro termo e a razão é igual a 2. Calcule a soma dos 15 termos.

Dados

• n=15
• a₁=2
• r=2
• S₁₅-?

Para calcular a soma dos 15 termos, primeiramente devemos calcular o a₁₅. Sendo assim, temos:

a_n=a₁+(n-1).r

a₁₅=2+(15-1).2

a₁₅=2+14.2

a₁₅=30

Fórmula da soma dos n termos:

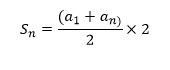
Calculando a soma do 15 primeiros termos, temos:

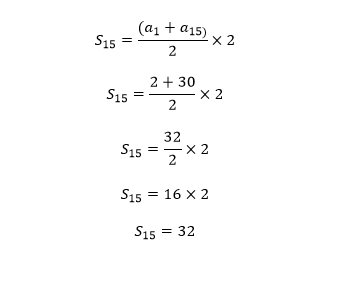
Portanto, a soma dos primeiros 15 termos é 32.

Exercícios sobre progressão aritmética (PA)

Os problemas que envolvem PA podem aparecer de varias formas, pois está ligada ao dia a dia. Observe os seguintes problemas abaixo:

1- Em uma PA, o quarto termo é 12 e o décimo termo é 28. Qual é a razão dessa progressão aritmética?

Resolução

Vamos resolver esse problema utilizando as fórmulas da progressão aritmética. Seja a razão da progressão aritmética r e o primeiro termo a1. Sabemos que o quarto termo é dado por:

a₄ = a₁ + 3r = 12

E o décimo termo é dado por:

a₁₀ = a₁ + 9r = 28

Agora vamos resolver esse sistema de equações. Primeiro, vamos encontrar o valor de a1 e depois a razão r.

a₁ + 3r = 12
a₁ + 9r = 28

Subtraindo a primeira equação da segunda equação, obtemos:

6r = 16
r = 16/6
r = 8/3

Portanto, a razão da progressão aritmética é 8/3.

LEIA TAMBEM:

• PRINCIPIO DA INDUÇÃO FINITA

• PROBLEMAS SOBRE EQUAÇÃO DO 1º GRAU