Denomina-se Equação do Primeiro grau com uma incógnita a toda igualdade entre expressões algébricas, que se transforma numa identidade numérica somente para um ou mais valores atribuído. As equações podem apresentar uma ou mais incógnitas (variáveis).
Leia:
Equação do 1º grau com uma incógnita é toda equação que pode ser escrito da seguinte forma: ax+b=c, onde a, b e c são números quaisquer e a≠0.
Por exemplo: 2x+1=0 x-12=6
Equações do 1º grau equivalentes
Duas ou mais equações são equivalentes quando admitem as mesmas soluções ou mesmos conjuntos verdade.
Por exemplo:
- x+5=7; solução x=2
- 3x-1=5; solução x=2
Resoluções das equações do primeiro grau com uma incógnita
Para resolver uma equação do primeiro grau com uma incógnita, aplicaremos alguns procedimentos algébricos da seguinte forma:
a) Se as equações possuírem parenteses eliminam-se os parentes;
b) Se as equações possuírem termos fracionários eliminam-se os denominadores;
c) Isolam-se num dos membros todos os termos que contêm a variável e, do outro, os termos sem variáveis (termos independente);
d) Reduzem-se os termos semelhantes;
e) Determina-se o valor da variável (incógnita);
f) Representação da solução;
Por exemplo:
1º x+2(x+1)=26
x+2x+2=26
x+2x=26-2
3x=24
x=24/3
x=8
S= {8}
2º 4x+3=2x+11
4x-2x=11-3
2x=8
x=8/2
x=4
S= {4}
3º
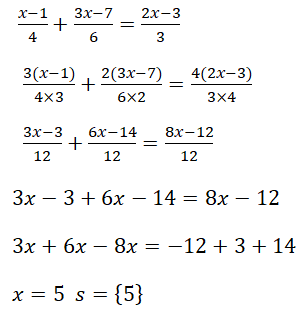
Leia também:
Problemas que envolvem equação do primeiro grau com uma incógnita
1. Pelé pagou 70kzs por um lápis e uma esferográfica, sabendo que o lápis custou 20kzs. Quanto custou a esferográfica.
Resposta
Para este problema, nós precisamos descobrir qual é o valor da esferográfica. Neste caso a nossa incógnita é o valor da esferográfica, atribuindo x na incógnita teremos:
x+20=70
x=70-20
x=50
S={50}
Portanto o valor da esferográfica é 50kzs
2. A soma de dois números consecutivos é 25. Qual é o valor do menor número?
Resposta
Números consecutivos são números que se encontram imediatamente um apos do outro. Neste caso como não se sabe qual é este número, vamos considerar como uma incógnita x, se x é o número então o seu sucessor é x+1, assim temos:
x+(x+1)=25
x+x+1=25
2x=25-1
2x=24
x=24/2
x=12
S= {12}
Portanto o número em causa é 12.
3. A metade de um número adicionando 2 é igual a um terço deste número adicionando 3. Qual é este número?
Resposta
O número em causa não é especificado, neste caso vamos considerar como variável x. Entretanto metade de um número neste caso é x escrevemos x/2 e um terço escrevemos x/3, assim temos:
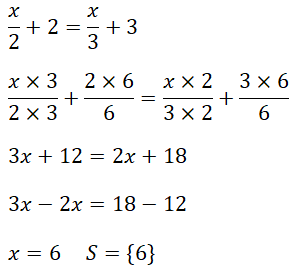
Portanto o número procurado é 6.
4. A senhora Ana foi a super mercado e comprou carne no valor de 1000kzs e arroz de 1500kzs, tendo regressado a casa com 600kzs. Calcula o valor que a senhora Ana levou ao super mercado.
Resposta
x-1000-1500=600
x=600+1000+1500
x=3100 ; S= {3100}.
Portanto a senhora Ana levou 3100kzs.
Veja também :