Funções Racionais

Toda função do tipo 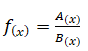em que A(x) e B(x) são polinómios em x , sendo B(x) diferente de zero, chama-se funções racionais ou fraccionarias.

Leia também:

Números Racionais

Domínio ou condições de existencias das funções racionais

Quanto ao domínio de uma função fraccionaria , B(x) pertence ao conjunto dos números reias, excepto zero. De forma resumida, temos:.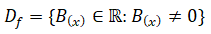

Por exemplo:

Determine o domínio da seguinte função racional:

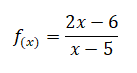
Dominio da função racional ou fraccionaria

Quanto ao dominio da função racional, o denominador tem de ser diferente de zero. Sendo assim, temos:

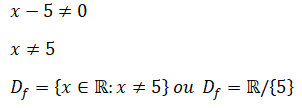
Portanto, o valor de x tem de ser valores diferentes de 5. Por sua vez x= 5 é a assimptota vertical da função.

Classificação das funções racionais

Quanto a classificação das funções fraccionarias podem ser:

• Próprias: Quando o qrau do numerador for maior que o grau do denominador;
• Impróprias: Quando o grau do numerador for maior ou igual ao grau do denominador.

Exercícios

Dodo as funções fraccionarias abaixo, determine o domínio:

a).

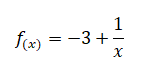
Resolução

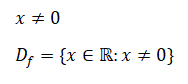
b).

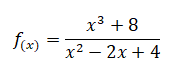
Resolução

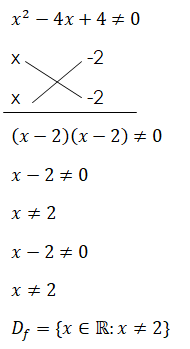
c).

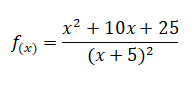
Resolução

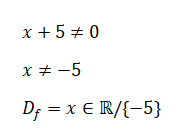
Leia também :

Equações do 1º grau