Chama-se sistema de duas equacoes do 1º grau em x e y, ao conjunto de duas equações na forma canónica:
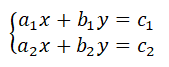
Leia também:
Sendo a, b e c números reais, isto é, a e b não podem ser simultaneamente igual a zero. Este sistema de duas equações lineares, também pode-se escrever da seguinte forma: a1x+b1y=c1 e a2x+b2y=c2 .
Métodos de resolução do sistema de duas equações do 1º grau
Dado o sistema pretende-se resolve-lo, isto é, determinar os pares ordenados x e y. Para resolver o sistema de duas equações, temos que aplicar o princípio de equivalência, a cada uma das equações de forma que elas fiquem na forma canónica.
Posteriormente resolve-se o sistema de duas equações lineares utilizando os seguintes métodos:
- Método de Substituição;
- Métodos de Comparação;
- Métodos de Adição ou redução ao coeficiente simétricos;
- Método Gráfico;
- Método de Cramer.
Exercícios sobre sistema de duas equações do 1º grau
- Represente os seguintes sistema de duas equações lineares na forma canónica:
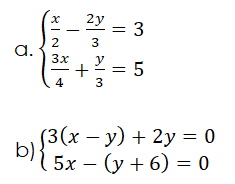
Resolução
Para escrever o sistema na forma canónica. Basta, eliminar os denominadores o sistema de duas equações . Sendo assim, temos:
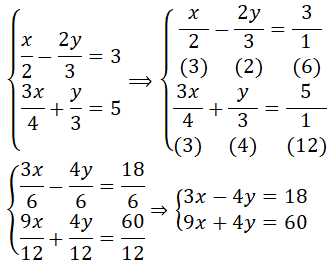
Logo, o sistema: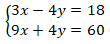
Resolução
Para escrever na forma canónica, basta eliminar os parenteses, aplicando a simplificação de expressões com parenteses. Sendo assim, temos:
- 3(x-y)+2y=0
- 5x-(y+6)=0
Simplificando os parenteses, temos:
- 3x-3y+2y=0
- 5x-y-6=0
Passando os termos com variáveis no 1º menbro e os que nao têm variáveis no segundo menbro, temos:
- 3x-5y=0
- 5x-y=6
Portanto, o sistema: 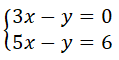
Leia também:


