Quando estamos diante de dois intervalos, quer dizer que eles ou têm um ponto ou vários pontos em comum ou simplesmente não tem nenhum ponto em comum. Para isso observamos como indicar a intersecção e reunião de intervalos.
Leia também:
Para determinar a intersecção e reunião de intervalos é necessário recorrer a representação gráfica ou geométrica para facilitar a indicação da intersecção e reunião de dois intervalos. Sendo assim, temos:
INTERSECÇÃO DE INTERVALOS
A intersecção ou seja ligação de dois intervalos é um intervalo constituído pelos pontos comuns aos dois intervalos.
Por exemplo:
Dados os intervalos A e B. Indique a sua intersecção:
a)……A=]2;4] e B=]3;5]
Resolução
Para indicar a intersecção dos dois conjuntos, basta representar graficamente os dois conjuntos. Sendo assim, temos:
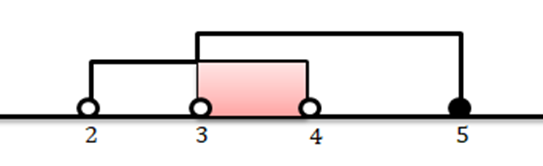
Neste caso, os dois intervalos começaram a intersectar-se a partir do intervalo aberto de 3 até o intervalo aberto de 4.
Portanto: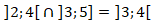
b)…….A=]2;4[ e B=]4;5[
Resolução
Para indicar a intersecção dos dois conjuntos, basta representar graficamente os dois conjuntos. Sendo assim, temos:
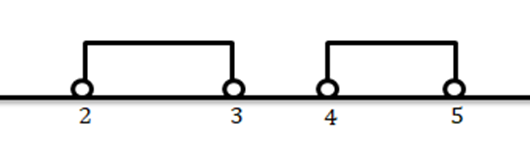
Visto que os dois intervalos não tem intersecções. Então, podemos dizer que a sua intersecção é vazio 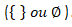
Logo: 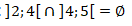
c)……A=]0;4[ e B=]1;2]
Resolução
Para indicar a intersecção dos dois conjuntos, basta representar graficamente os dois conjuntos. Sendo assim, temos:
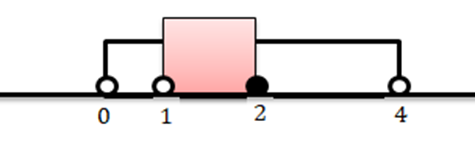
Neste caso, os dois intervalos começaram a intersectar-se a partir do intervalo aberto de 1 até o intervalo fechado de 2.
Portanto: 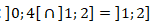
A conjunção de intervalos corresponde a conjunção de condições.
REUNIÃO DE INTERVALOS
A reunião ou juncão de dois intervalos é o conjunto de constituído pelos elementos comuns e não comuns dos intervalos.
Por exemplo:
Dados os intervalos A e B. Indique a reunião.
a)……A=]2;4[ e B=]3;5]
Resolução
Para indicar a reunião dos dois conjuntos, basta representar graficamente os dois conjuntos. Sendo assim, temos:
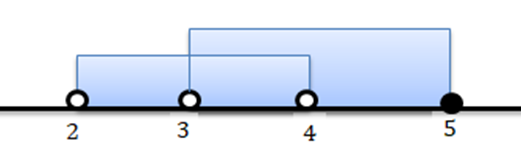
Neste caso, a reunião dos dois intervalos começa do intervalo aberto de 2 até ao intervalo fechado de 5.
Portanto: ]2;4[ U]3;5]= ]2;5].
b)…..A=]2;4[ e B=]4;5[
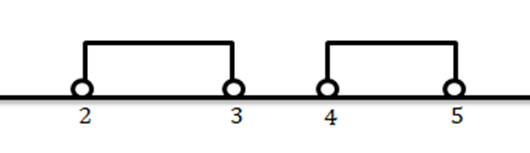
Neste caso, a reunião dos dois intervalos é o intervalo de 2 a 3 união com o intervalo aberto de 4 a 5.
Logo: AUB=]2;4[U]4;5[ .
A reunião de intervalos corresponde a disjunção de condições.
EXERCÍCIOS SOBRE INTERSECÇÃO E REUNIÃO DE INTERVALOS
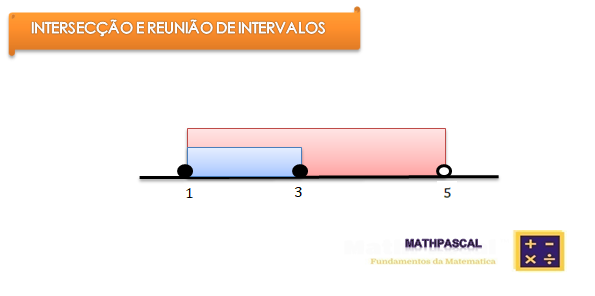
1-Dados os intervalos A e B , indique 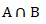
A=[1;5] e B=]2;3]
2-Dados os intervalos A e B, indique AUB:
A=]1;3] e B=[1;5[
Resolução
Resolução (1)
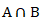
A=[1;5] e B=]2;3]
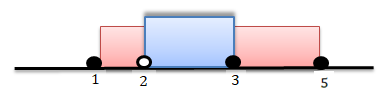
Portanto: 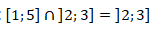
Resolução (2)
AUB:
A=]1;3] e B=[1;5[
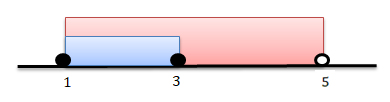
Portanto: ]1;3]U[1;5[.
Leia também: