Uma equação do 1º grau a duas incógnitas, é toda equação do tipo ax + by =c, em que a, b e c são números reais, sendo a e b diferente de zero.
Aprenderás também sobre:
Observe o seguinte exemplo: Um triângulo isósceles sabe-se que tem perímetro igual 10 unidades de comprimento. Como será o triângulo?
Visto que um triângulo isósceles tem dois lados iguais, temos:
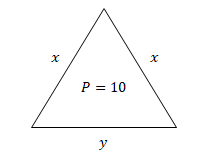
O perímetro de um triângulo é igual ao somatório dos seus lados. Sendo assim, temos: P= x + x + y—>
2x + y = 10. Sendo assim, obtemos uma equação do 1º grau a duas incógnitas.
Método de resolução da equação do 1º grau a duas incógnitas
Visto que toda equações do 1º grau a duas incógnitas têm infinitas soluções. Então, para resolver este tipo de equação, determinar todos os pares ordenados possíveis que verificam a equação.
Por exemplo: Considere a seguinte equação: 2x + y = 10. De entre os pares ordenados (x; y) de números, indique os que são solução da equação: (0;10), (3;5), (4;9) ,(1;8) e (5;0).
Resolução
Para verificar o pares ordenados se são solução da equação. Basta substituir cada par ordenado na equação do 1º grau a duas incógnitas. Sendo assim temos:
(0;10)….Este par ordenado, é composto pelas coordenadas x e y.
X=0 e y=10. Substituindo na equação, temos:
2x + y = 10
2.0+10=10
0+10=10
10=10
(3;5)
X=3 e y=5. Substituindo na equação, temos:
2x + y = 10
2.3+5=10
6+5=10
. 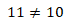
(4;9)
x=4 e y=9. Substituindo na equação, temos:
2x + y = 10
2.4+9=10
8+9=10
. 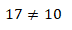
(1;8)
x=1 e y=8. Substituindo na equação, temos:
2.1 + 8 = 10
2+8=10
10=10
(5;0)
x=5 e y=0. Substituindo na equação, temos:
2.5 + 0 = 10
10+0=10
10=10
São soluções da equação os pares ordenados: (0;10), (1;8) e (5;0).
Também podemos representar geometricamente ou graficamente os pares ordenados que verificam a equação ou simplesmente a equação do 1º grau a duas incógnitas.
Interpretação geométrica da equação do 1º grau a duas incógnitas
Para representar geometricamente a equação do 1º grau a duas variáveis, deve-se isolar a variável y na equação .
Por exemplo:Resolve a equação 2x+y=10 em ordem a variável y e represente-a graficamente.
Resolução
Para representar a equação 2x+y=10. Primeiramente isola-se a incógnita y na equação. Sendo assim, temos:
2x+y=10
Y=-2x+10
Posteriormente, atribuem-se valores a variável x, para encontrar o valor de y. Preenchendo a tabela, temos:
de y. Preenchendo a tabela, temos:
| X | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| y | 10 | 8 | 6 | 4 | 2 | 0 | -2 | -4 | -6 |
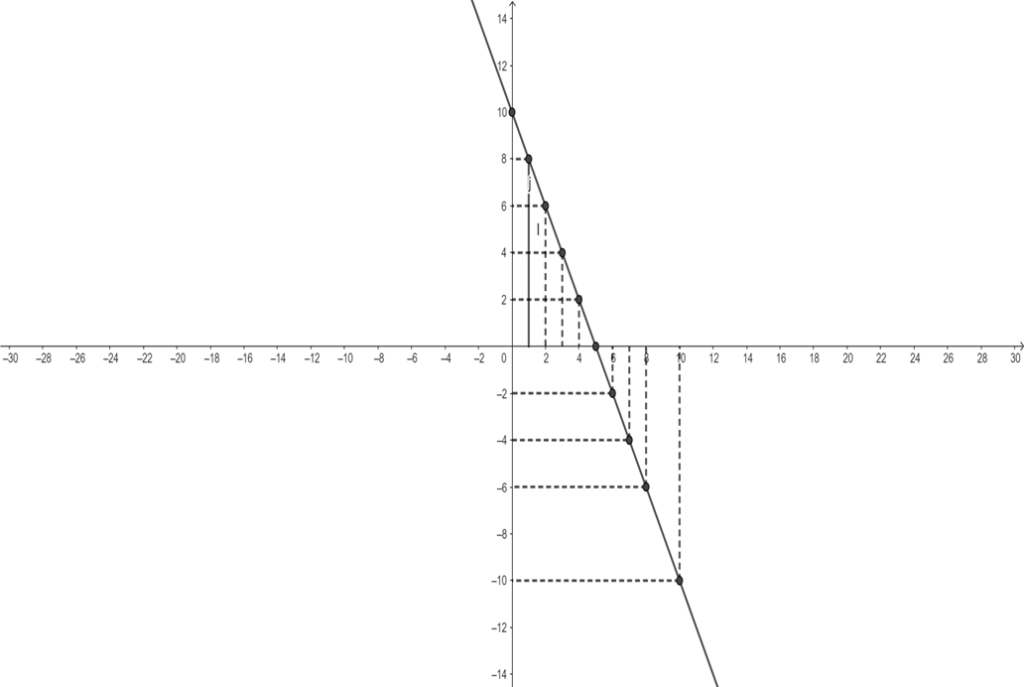
Portanto, a equação 2x+y=10, tem infinitas soluções:
(0;10),(1;8),(2;6),(3;4),(4;2),(5;0),(6;-2),(7;-4),(8;-6),…todos os pares ordenados da equação 2x+y=10 são soluções da equação.
Exercícios sobre equação do 1º grau a duas incógnitas
- Considere a equação:
X-3y=7
- De entre os pares ordenados (x;y) de números, indique os que são solução da equação (1;-2),(7;0),(8;-1),(4;1).
2. Considere a equação:
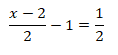
- Resolva a equação em ordem a y e represente-a geometricamente.
1.Resolução
(1;-2)
X=1 e y=-2. Substituindo na equação, temos:
x-3y=7
1-3(-2)=7
1+6=7
7=7
(7;0)
X=7 e y=0. Substituindo na equação, temos:
x-3y=7
7-3.0=7
7=7
(8;-1)
x=8 e y=-1. Substituindo na equação, temos:
x-3y=7
8-3(-1)=7
8+3=7
.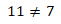
(4;1)
x=4 e y=1. Substituindo na equação, temos:
x-3y=7
4-3.1=7
. 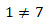
Logo, são soluções da equação os pares ordenados: (1;-2) e (7;0).
2.Resolução
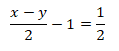
Isolando a variável y na equação, temos:
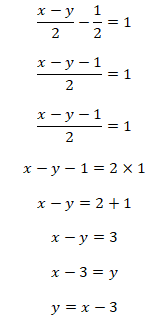
| x | 0 | 1 | 2 |
| y | -3 | -2 | -1 |
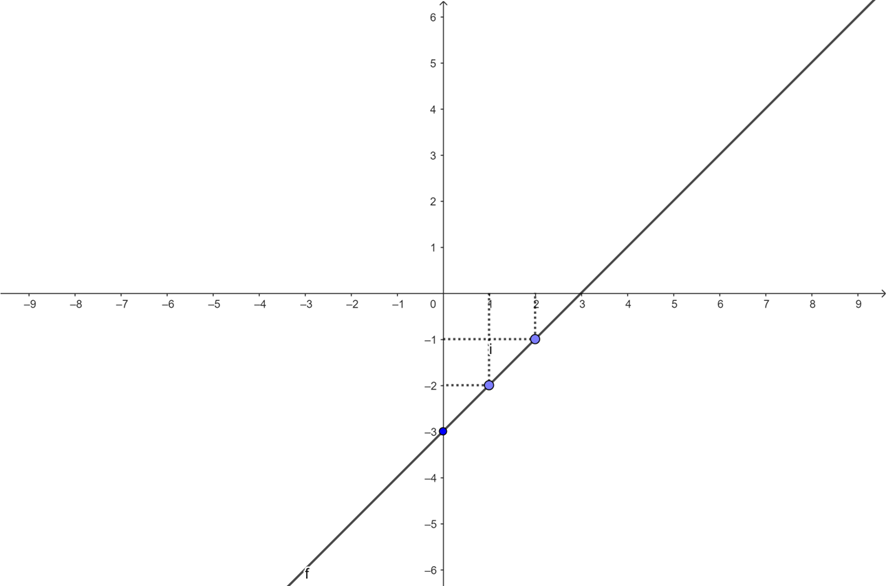
Portanto, a equação 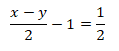
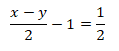
Leia também:


