A secção da teoria dos números conhecida como principio da indução finita (PIF) visa demonstrar e verificar se as propriedades ou formulas de uma sucessão específica são verdadeiras. O PIF é uma proposição verdadeira clara para caracterizar o conjunto de números naturais (P(n).
O princípio da indução finita exige a verificação de dois componentes essenciais:
- Base da indução P(1): A proposição é verdadeira para n=1;
- Passo indutivo ou hipótese P(k): A proposição é verdadeira para n=k…P(k), então também é verdadeira para n=k+1…P(k+1).
Obs.: Para demonstrar uma determinada propriedade , é necessário ter domínio da matemática fundamental sobre tudo sucessões numéricas.
Exemplo: Demonstrar por indução matemática: 1^2+2^2+3^2+…+n^2=n(n+1)(2n+1)/6
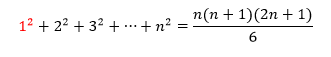
Resolução
Para começar, precisamos igualar a expressão do membro direito acima por p(n):
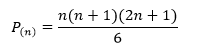
A base da indução
Consiste em determinar se a solução deve ser o primeiro valor da expressão solicitada para demonstrar quando atribuímos um valor inicial na propriedade ( 12).Para confirmar a base, atribua n=1 à expressão:
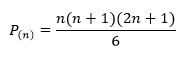
Sendo assim, temos:
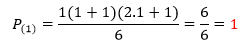
P(1) = 1.
Isso demonstra que p(1) é a resposta do primeiro termo, que é 1.
A hipótese da indução
Consiste em verificar que a expressão será igual à propriedade anterior para n=k. Assim, supondo que n=k seja verdadeira, temos:
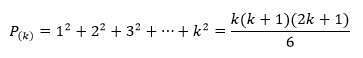
Podemos confirmar que a expressão “encontrada” é correta porque corresponde à propriedade original.
Finalmente, p(k+1) também é verdadeira. Assim, temos:
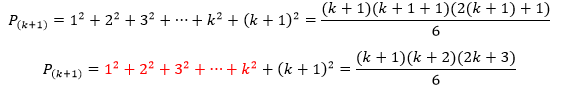
Essa expressão: 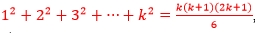
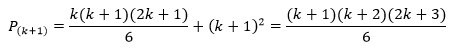
Agora, vamos verificar se o membro esquerdo e o direito são iguais. Fazendo as contas, obtemos:
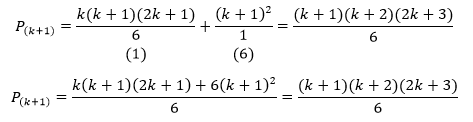
Fautorizando a expressão (k+1), temos:
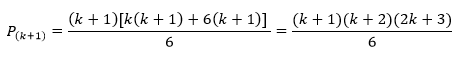
O membro esquerdo corresponde ao membro direito, então, pelo principio de indução finita (PIF), a igualdade vale para todo número natural n maior ou igual a 1.
Exercícios sobre principio de indução finita
- Demosntrar que para todo inteiro positivo n,
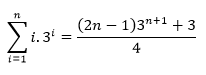
Com conhecimento da expressão acima, pode-se escrever da seguinte forma:
Para i=(1,2,3,…) encontramos:
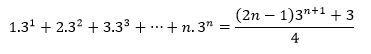
Base da indução : n=1
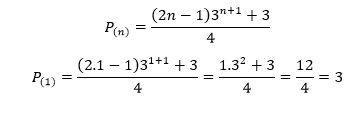
O primeiro termo da sequencia, p(1)=3, pode ser observado.
Tese da Indução: Se assumirmos que p(k) é verdadeira, então temos: n=k.
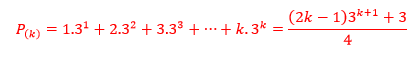
Além disso, precisamos demonstrar que p(k+1) também é verdadeira, portanto, temos: n=k+1.
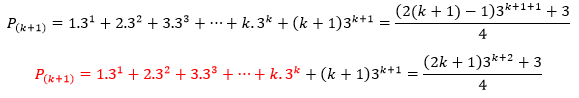
Sabendo que:
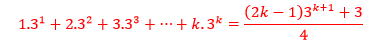
Substituindo na expressao acima, temos:
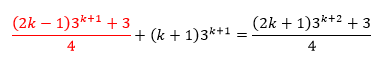
Igualando aos mesmos denominadores temos:
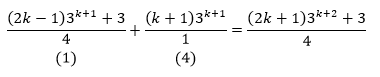
Colocando em evidencia o factor comum 3^k+1, temos:
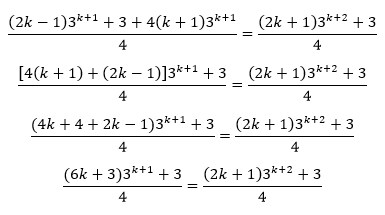
Factorizando a expressao 6k+3=3(2k+1), temos
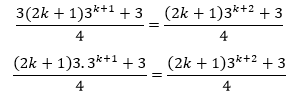
Efectuando a propriedade da potencia na expressao 3. 3^k+1= 3^k+2, temos:
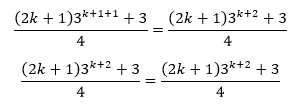
Logo podemos verificar, usando o PIF, que a igualdade é válida para todo n maior que 1.
LEIA TAMBEM:


