Com esta temática saberás tudo sobre as principais operações com conjuntos, tais como: interseção de conjuntos; reunião de conjuntos; diferença de conjuntos e complementar de um conjunto.
Para a melhor compreensão desta temática, é importante que leia o artigo referente à Conjuntos.
Nesta aula, poderás aprender:
- Reunião de conjuntos
- Propriedade da União de Conjuntos
- Interseção de conjuntos
- Propriedade da Interseção de Conjuntos
- Diferença de conjuntos
- Propriedade da Diferença de Conjuntos
- Complemenar de um conjunto
- Propriedade do Complemento de Conjuntos
União de dois ou mais conjuntos
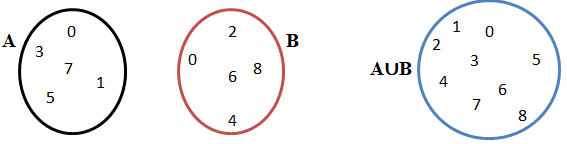
Dados dois conjuntos A e B, chamamos de união ou reunião de A com B o conjunto formado pelos elementos que pertencem ao conjunto A ou ao conjunto B. Simbolicamente indicamos esta operação por A∪B.
Por exemplo: A = {0, 1, 3, 5, 7} B = {0, 2, 4, 6, 8}
A∪B = {0, 1, 2, 3, 4, 5, 6, 7, 8}
Propriedade da União de Conjuntos
1º A ∪ ∅ = A
2º A ∪ B = B ∪ A
3º A ∪ A=A
4º (A ∪ B) ∪ C = A ∪ (B ∪ C)
Interseção de dois ou mais conjuntos
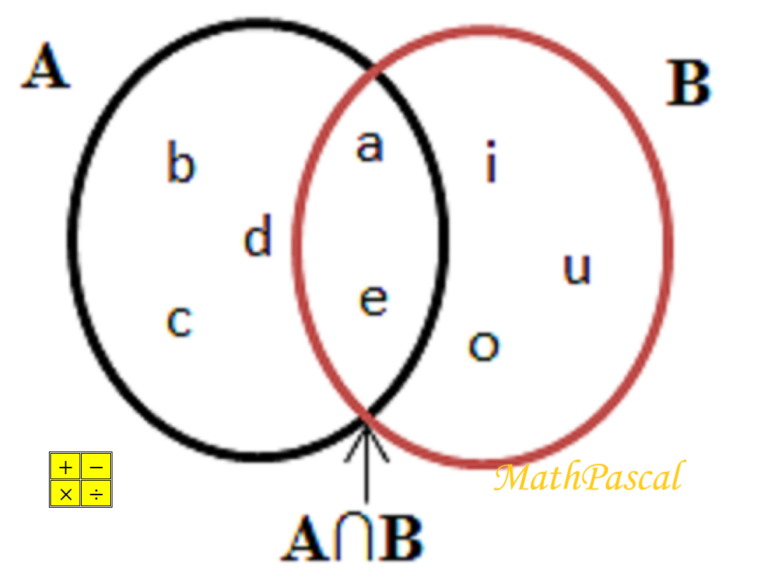
Dados dois conjuntos A e B, chamamos de interseção de dois conjuntos A e B o conjunto formado pelos elementos que pertencem a A e a B. Simbolicamente indicamos esta operação por A∩B.
Por exemplo: A = {a, b, c, d, e} B = {a, e, i, o, u}
A∩B = {a, e} 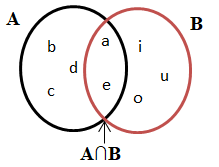
Propriedade da Interseção de Conjuntos
1º A ∩ ∅ = ∅
2º A ∩ B = B ∩ A
3º (A ∩ B) ∩ C = A ∩ (B ∩ C)
Diferença de conjuntos
Dados dois conjuntos A e B, chamamos de diferença entre dois conjuntos A e B o conjunto formado pelos elementos de A que não pertencem a B. Simbolicamente indicamos esta operação por A-B.
A – B = {x/x ϵ A e x ∉ B}.
Por exemplo: Dados os conjuntos A = {1, 4, 5} e B = {2, 4, 8}, determina a diferença de A e B.
Representando no diagrama de venn, temos:
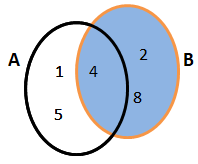
A definição da diferença de conjuntos A e B, realsa que será um conjunto formado pelos elementos que pertecem ao conjunto A e não pertecem ao conjunto B. A partir do diagrama de Venn, conseguimos observar que os elementos que pertecem a A e não a B são 1 e 5, portanto a diferença de A por B é o conjunto {1, 5}, ou seja, A – B = {1, 5}.
Propriedade da Diferença de Conjuntos
1º Se A ∩ B = ∅, então A – B = A
2º Se B ⊂ A, então B – A = ∅
3º Se A ≠ B, então A – B ≠ B – A
4º Se A = B, então A – B = ∅ e B – A = ∅
Complemenar de um conjunto
Dados dois conjuntos A e B, em que B ⊂ A, chamamos de complementar de B em relação a A o conjunto formado pelos elementos que pertencem a A e não pertencem a B, ou seja, A – B. Simbolicamente indicamos esta operação por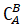
Diante disto é importante perseber que para determinarmos o complementar de um conjunto qualquer, primeiro devemos saber que entre os conjuntos em causa, um deles deve ser um subconjunto do outro.
Por exemplo: Dados os conjuntos A = {2, 3, 5, 7} e B = {3, 7}, determina o complementar de B em relação a A.
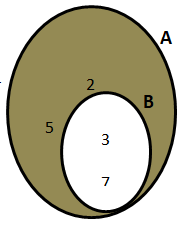
Como vemos B está incluso em A, ou seja, B ⊂ A. Para encontrarmos o que precisamos, basta encontrar A – B, ou basta responder a seguinte pergunta: Que elementos faltam ao conjunto B para que o conjunto B seja o conjunto A?
Como A – B = {2, 5}, logo O complementar de B em relação a A é {2, 5}.
Propriedade do Complemento de Conjuntos
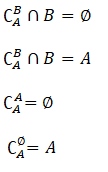
Exercícios sobre operações com conjuntos
1- Dados os seguintes conjuntos: A={1,4,5} B={2,4,8} C={2}
a) Determina:
A∪C = A∩B =
B∪C = C∩B =
2- Dados os conjuntos: A = {1, 2, 3, 4, 5} B = {2, 4, 6, 8} C = {2, 4, 5, 7}, determina.
a) A-B b) B-C c) C-A
3- Dados A = {a, e, i, o} B = {a, e, i} C = {a, e, i, o, u}
a) Complementar de A em relação a C
b) Complementar de B em relação a A
c) Complementar de B em relação a C
Resposta dos exercícios sobre operações com conjuntos
1- a) A∪C = {1, 2, 4, 5} A∩B = {4} B∪C = {2, 4, 8} C∩B = {2}
2- a) A-B = {1, 3, 5} b) B-C = {6, 8} c) C-A = {7}
3- a) {u} b) {o} c) {o, u}