Ao resolver um sistema de duas equações do 1º grau a duas incógnitas aplicando o método gráfico, procura-se determinar os valores das incógnitas x e y. O método gráfico consiste em representar graficamente as duas equações no sistema cartesiano.
Leia também:
Passos para resolver o sistema de duas equações do 1º grau a duas incógnitas pelo método gráfico
Para resolver um sistema de equações aplica-se os seguintes passos:
- Resolver cada uma das equações do sistema em ordem a y. Isto, transformar numa função;
- Representar as rectas associadas a cada uma das equações que formam o sistema dado, no mesmo referencial;
- Procurar no gráfico, se existirem, pontos comuns as duas rectas.
Observação: Para facilitar nos cálculos é necessário que escreva o sistema de equação na forma canónica caso não esteja.
Leia também:
Classificação do sistema de duas equações do 1º grau
O sistema de duas equações lineares classifica-se em:

No sistema possível determinado, as rectas são Concorrentes, no sistema possível indeterminado as recta são Coincidentes e no sistema impossível as rectas são Paralelas.
Por exemplo:
Resolve o seguinte sistema de equações aplicando o método de grafico:
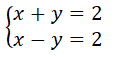
Resolução
Resolve-se cada uma das equações do sistema em ordem a y. Sendo assim, temos:
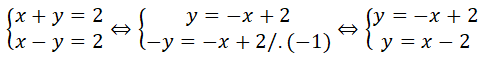
Posteriormente, faz-se a representação gráfica das rectas associadas a cada uma das equações. Para isso, deve-se prencher a tabela de valores das duas equações. Sendo assim, temos:
1ª equação:
Y=-x+2
| X | 0 | 1 | 2 |
| Y | 2 | 1 | 0 |
2ª equação :
Y=x-2
| X | 0 | 1 | 2 |
| Y | -2 | -1 | 0 |
Representando no sistema cartesiano, temos:
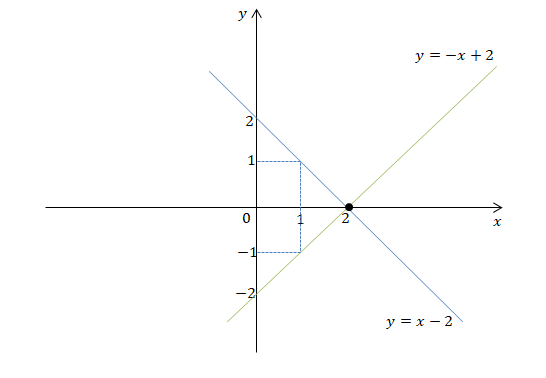
As rectas y=-x+2 e y=x-2 são concorrentes no ponto (2;0). O sistema tem uma única solução, é um sistema possível determinado.
Verificação da solução do sistema
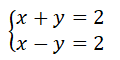
Substitui-se, em cada equação do sistema dado: x=2 e y=0. Sendo assim, temos:
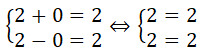
Portanto a solução do sistema dado é o par de números (2;0)
Exercícios sobre sistema de duas equaçõesdo 1º grau a duas incógnitas aplicando o método gráfico
1.Resolve graficamente o seguinte sistemas de equações:
a)-Resolver graficamente o sistema:
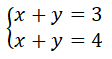
b)-Classificar o sistema
Resolução
A equação x+y=3 é equivalente a y=-x+3.
A equação x+y=4 é equivalente a y=-x+4.
y=-x+3
| X | 0 | 1 | 2 | 3 |
| y | 3 | 2 | 1 | 0 |
y=-x+4
| X | 0 | 1 | 2 | 3 |
| y | 4 | 3 | 2 | 1 |
Representando os pares ordenados no sistema cartesiano, temos:
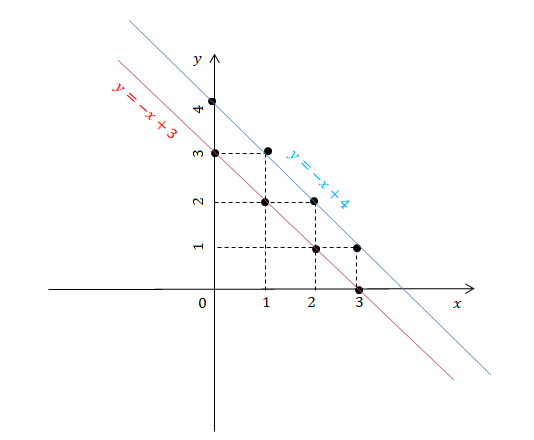
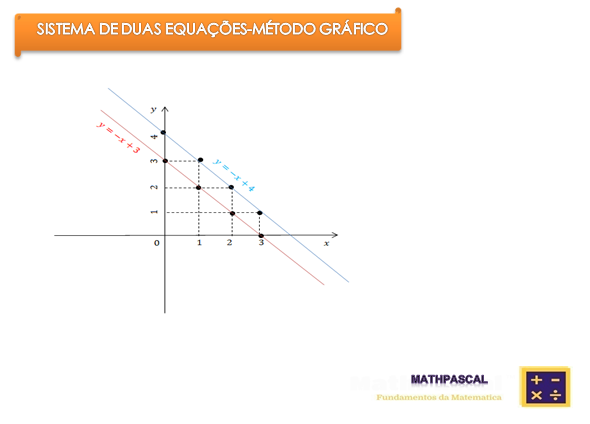
Observamos pelo gráfico que as rectas y=-x+3 e y=-x+4 são paralelas, não tendo qualquer ponto em comum.
b) Dizemos, por isso, que o sistema é impossível.
2-Resolver graficamente o sistema 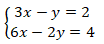
Resolução:
Observando o sistema, vemos que podemos dividir ambos os membros da 2ª equação por 2, obtendo-se um sistema equivalente mais simples.
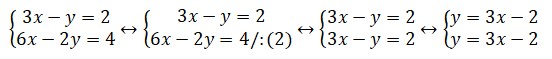
O sistema dado reduz-se a uma só equação do 1º grau com duas incógnitas, que vamos representar graficamente:
| X | 0 | 1 | 2 |
| y | -2 | 1 | 4 |
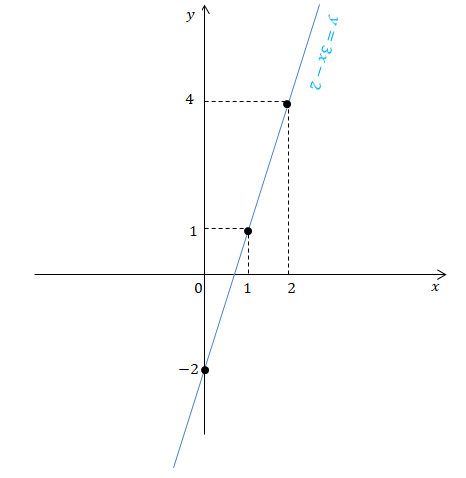
O sistema dado tem uma infinidade de soluções, ou seja, todos os pontos da recta y=3x-2. Potanto , as rectas são coincidentes ;O sistema é possível e indeterminado.
Leia também: