Sabe-se que o inverso da multiplicação é a divisão. A divisão de números fraccionários, é feita do seguinte modo: Mantem-se a primeira fracção e multiplica-se pelo inverso da segunda fracção.
Leia: Multiplicação de números fraccionários
Exemplo:
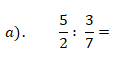
Neste caso, apenas mantem-se a primeira fracção 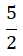
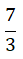
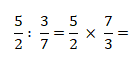
Posteriormente, multiplica-se os numeradores (5×7) e os denominadores (2×3). Assim, temos:
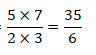
Propriedades da divisão de números fraccionários
Na divisão de números fraccionários não apresentam as propriedades: associativa, comutativa e distributiva. Porque nestas propriedades, altera-se a ordem e na divisão se alterar as ordem também alteram-se o resultado.
Elemento neutro da divisão: O elemento neutro da divisão é 1, porque todo numero dividindo por 1 dá o mesmo número. Assim temos: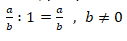
Exemplo:
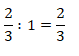
Inverso de um número: é a troca do numerador pelo denominador. Assim temos: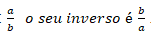
Exemplo:
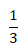
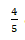
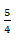
Problemas que envolvem divisão de números fraccionários
1- A EPAL ( Empresa de águas públicas de Luanda) conservou 500 litros de água e foram distribuída por recipientes de 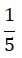
Resolução
Neste caso, devemos dividir 500 litros de água pelos recipientes que foram distribuídas 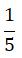
500: 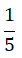
Estamos diante da divisão de números fracionários. Logo, deve-se manter a numero e multiplicar pelo inverso do segundo numero. Assim, temos:
Litros de água: 500
Recipiente : 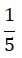
Posteriormente, efetuamos a multiplicação :
500×5=2500
Portanto, encheram 2500 recipientes.
2. A metade de um bolo de um aniversário foi dividida em 4 pessoas . Qual é a fracção que representa o bolo comido por cada pessoa ?
Resolução
Neste contexto, a metade do bolo é 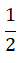
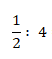
Estamos diante da divisão de fracções. Para resolver, mantem-se a primeira fracção 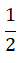
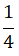
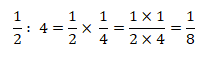
Portanto, cada pessoa comeu 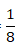
Exercícios resolvidos
- Calcule:
a). 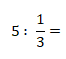
b). 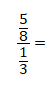
Resolução
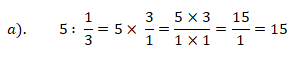
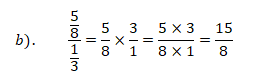
Leia também :
Conjunto dos números racionais