Números fracionários são expressões compostas por numerador e denominador. A adição de números fraccionários acontece de dois modos: Adição de fracções com o mesmo denominador e adição de fracções com denominadores diferentes.
Ver: Conjunto dos números racionais
Adição de fracções com o mesmo denominador: Adiciona-se os numeradores e mantem-se o denominador comum. Assim, temos: 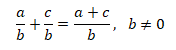
Exemplo:
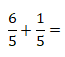
Os denominadores são iguais. Portanto, mantem-se o denominador comum e adiciona-se os numeradores. Neste caso, temos:
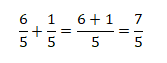
Adição de fracções com denominadores diferentes: Acha-se os denominadores comuns. Posteriormente, adiciona-se os numeradores e mantem-se os mesmos denominadores . Assim, temos:
Exemplo:
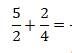
Os denominadores são diferentes. Neste caso, devemos achar os mesmos denominadores. Para isso, determina-se o mínimo múltiplo comum dos denominadores ou seja m.m.c. (2;4)=4. Assim, temos:
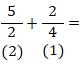
Posteriormente, multiplica-se os números que estão dentro de parênteses (2) e (1) com os numeradores (5) e (2) e pelos denominadores (2) e (4) . Neste caso, temos:
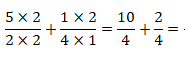
Finalmente, encontramos os mesmos denominadores. Para isso, adiciona-se o numeradores (10+2) e mantem-se o denominador comum (4). Assim temos:
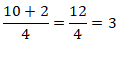
Observação: Quando tiver mais de uma fracção, deve-se agrupar em grupo de duas fracções, parar facilitar os cálculos.
Propriedades da Adição de números fraccionários
Nas propriedades da adição, pode-se alterar a ordem, mas não alterará o resultado. Sendo assim, temos:
Comutativa: Numa soma de números fraccionários a ordem das parcelas é arbitrária. A adição de números fraccionários é uma operação comutativa. Assim, temos: 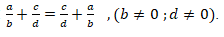
Exemplo: 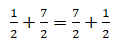
Associativa: A ordem de duas adições sucessivas de números fraccionários não importa. A adição de números fraccionários é associativa. Assim, temos: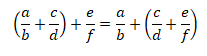
Exemplo: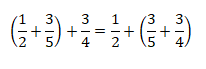
Elemento neutro: Tem um elemento aditivo no conjunto dos números racionais, que é o algarismo zero. Deste modo, temos: 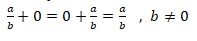
Exemplo: 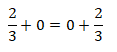
Problema que envolvem adição de fracções
1. Um jogador do Clube Petro Atlético de Luanda corre numa determinada pista do estádio 11 de Novembro. No primeiro dia corre 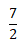
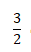
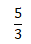
Resolução
Para determinar o numero de volta que o jogador deu : inicialmente, devemos identificar as três fracções referente ao numero de voltas. Assim, temos:
Primeiro dia 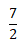
No segundo dia 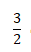
No no último dia 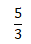
Seguidamente, adicionamos as três fracções. Deste modo temos:
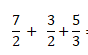
Visto que estamos diante da adição de três fracções , para facilitar os cálculos vamos agrupar as fracções em grupo de dois. Sendo assim temos:
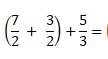
Calcula-se as fracções que estão dentro de parênteses. Visto que são fracções com mesmo denominador, adiciona-se os numeradores e mantem-se o denominador comum. Assim, temos:
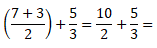
Agora estamos diante da adição de fracções com denominadores diferentes. Para isso, reduz-se as fracções ao mesmo denominador ( acha-se o denominador comum) . Assim, temos:
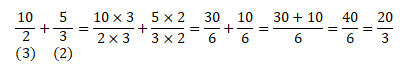
Portanto, a fracção que representa o total de voltas é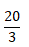
Exercícios resolvidos
1. Resolve as seguintes fracções em Q:
a). 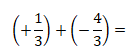
b). 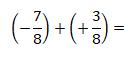
Resolução
a).
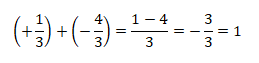
b).
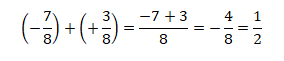
Leia : Adição de números inteiros
2.Um estudante do ISCED Sumbe, obteve as seguintes notas: Na primeira obteve 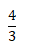
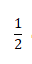
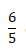
Resolução
Para determinar a fracção que representa o total das notas, apenas deve-se adicionar as fracções da primeira, segunda e terceira prova. Neste caso, temos:
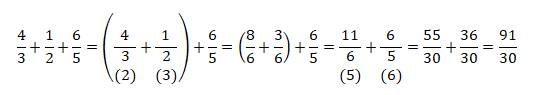
Portanto, a fracção que representa o total das notas é 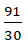
Leia também:


