A simplificação de expressões com parênteses acontece de três modos:
Leia também:
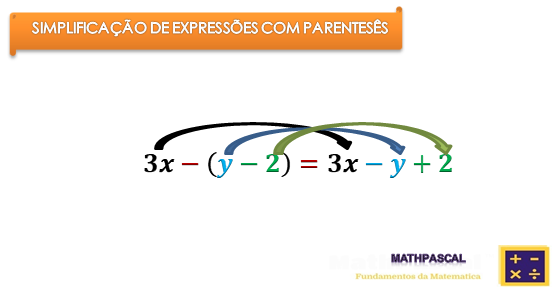
Quando o sinal negativo ( – ) aparece antes dos parênteses
Para simplificar expressões com parênteses que aparecem depois do sinal de diminuição (-), apenas eliminam-se os parênteses e trocam-se os sinais dos termos que estão dentro de parenteses: k – ( x + c ) = k – x – c.
Por exemplo:
a) 3x – (4x + 6 ) = 3x – 4x – 6 = -x – 6
b) 7x – (-5x -2 ) = 7x + 5x + 2 = 12x + 2
Quando o sinal positivo ( + ) aparece antes dos parênteses
Para simplificar expressões com parênteses que aparecem depois do sinal de adição (+), apenas eliminam-se os parênteses e mantem-se os sinais dos termos que estão dentro de parenteses: k + ( x + c ) = k + x + c.
Por exemplo:
a) 6x + (8x + 7 ) = 6x + 8x + 7 = 14x + 7
b) 3x + (-4x -2 ) = 3x – 4x – 2 = -x – 2
Quando o sinal de multiplicação (.) aparece antes dos parênteses
Para simplificar expressões com parênteses que aparecem depois do sinal da multiplicação (.), apenas eliminam-se os parênteses aplicando a propriedade distributiva: k .( x + c ) = k . x + k . c .
Por exemplo:
a) 2(3x + 4) = 2.3x + 2.4 = 6x + 8 = 6x + 8
b) 3.(-4x -2 ) = 3(-4x)+3(- 2) = -12x – 6
Exercicios sobre simplificação de expressões com parênteses
1-Simplifica as seguintes expressões:
a) 3(-2y+2)=
Neste caso, o numero 3, multiplica todos os termos que estao dentro de parênteses .Sendo assim, temos:
3(-2y) + 3.2 = -6y+6
b) ( 3x+4)-(-2x-7)=
Primeiramente, eliminam-se os parênteses obedecendo os critérios da simplificação de expressões com parênteses. Sendo assim, temos:
3x + 4 + 2x + 7 =
3x + 2x + 4 +7 = 5x + 11
c) (3x-20)+2(3x+8) =
Visto que a primeira expressão (3x-20) está antecedido do sinal de adição, apenas eliminam-se os prenteses da primeira expressão. Assim, temos: (3x-20)= 3x-20; Visto que a segunda expressão 2(3x+8) está antecidos por um número(2), para eliminar os parênteses aplica-se a propriedade distributiva. Sendo assim, temos:2(3x+8)=2.3x + 2.8 .
3x – 20 + 2.3x + 2.8 = 3x – 20 + 6x + 16 =
3x + 6x – 20 + 16 = 9x – 4
Leia também: