A 9ª classe representa um estágio de avaliação, visto que é o final do primeiro ciclo dos sitema de ensino do Ministério da Educção (MED) em Angola. Assim, os alunos enfrentam um exame que é criado pela direcção provincial de cada região. Portanto, com o intuito de auxiliar os estudantes na revião ou na obtenção de boas notas nas provas, foram organizados7 tópicos de conteúdos que saem no exame que tem aparecido com muita frequência nas provas de matemãtica da 9ª classe, entre os quais estão:
- Conjuntos dos números reais
- Cálculo em R
- Intervalos de números reais (limitados e ilimitados)
- Sitemas de duas equações a duas incógnitas (substituição , comparação , redução e gráfico)
- Problemas que envolvem sistemas de duas equações a duas incognitas
- Equação do 2º grau
- Inequação do 1º grau.
Mais abaixo, colocamos algumas questões que saem frequentemente no exame da 9 classe.
Algumas questões que saem no exame da 9ª classe
As perguntas incluem vários tópicos matemáticos de conteúdos que saem no exame e os mesmos são importantes para a avaliação.
1.Conjutos dos números reais
Este conteúdo é essencial no 9º ano, pois permite o aluno compreenda como agrupar objectos.Portanto, apresentamos a representação dos números reais na recta real:
Exemplo:
- Escreve por ordem crescente os seguintes números:
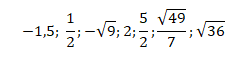
Leia também: Representação na recta real
2. Calculo em R
O cálculo em R refere-se a operações que envolvem o conjunto dos números reais.Aqui, apresentamos dois exercicios que costumam aparecer frequentemente nas avaliações, pois exigem que o estudante compreenda a decomposição em fatores primos, a simplificação de expressões com parenteses e tenha um bom domínio das quatro operações fundamentais da matemática.
Por exemplo:
- Realiza as operações seguintes, calculando em R:
a).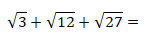
b).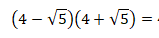
Leia também: Cálculo em R
3.Intervalos de números reais
Os intervalos de números reais foram criados para oferecer uma solução na representação por exetensão que não é viável dentro do conjunto dos números reais. Em relação ao conjunto dos números reais, há três formas de representá-los , que são:
Exemplo:
1.Dado os conjuntos:
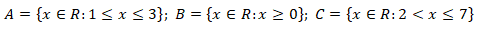
1.1. Represente-os sob forma de intervalo.
1.2. Determine:
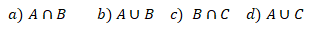
Leia também: Intervalos de números reais
4.Sitemas de duas equações a duas incógnitas
Relativamente a este subtema, geralmente não é comum aborda-lo para tratar directamente de um sistema. Ou seja, é necessãrio dominar ao menos um método para utilizar na resolução de propblemas que incluem sistemas do 1º à duas equações. Diante disso, apresentamos as seguintes questões:
Exemplo:
1.Resolve o seguinte sistema de duas equações :
- 2x-4y=6
- x+y=6
Leia também:
5.Problemas que envolvem sistemas de duas equações a duas incognitas
Após adquirires proficiência na resolução de conjuntos de duas equações usando qualquer um dos métodos analisados, agora estás preparado para lidar com questões relacionadas ao sistema de duas equações. Portanto, temos:
Exemplo:
- Um agricultor tem 240 galinhas em duas capoeiras, numa das capoeiras tem o dobro de galinhas que na outra. Quantas galinhas tem em cada copeira? ( Método a sua escolha)
6. Equações do 2º grau
- Resolve a seguinte equacao do 2º grau:
x2-4x+8=0
7. Inequação do 1º grau
1.Determine o conjunto solução da seguinte expressão:
6k-4(k-6)<30
Resolução dos exercicios que saem no exame da 9ª classe
Abaixo, temos a resolução dos exercicios propostos dos conteúdos que saem no exame com muita frequencia:
1. Resolução do exercício sobre conjunto dos números reais
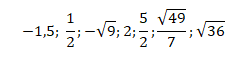
Para apresentar os números em ordem crescente, é necessário, inicialmente, simplificá-los. Portanto, se os números aparecerem como frações, precisamos dividi-los, e se estiverem na forma de raízes quadradas, precisamos calcular a raiz quadrada do número em questão. Assim, temos:
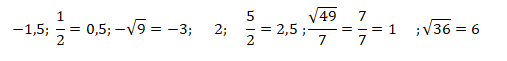
Posteriormente, representa-se os números na recta real. Sendo assim, temos:
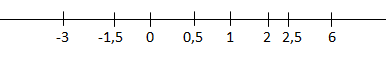
Organizando os números de forma crescente, temos:
C={-3;-1,5;0,5;1; 2; 2,5;6}
2. Resolução dos exercícios sobre cálculo em R
a)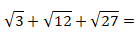
Decompondo os radicandos, temos:
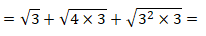
Aplicando a propriedade do produtos dos radicais ,temos:
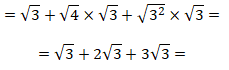
Adicionando os radicais com os mesmos radicando, temos:
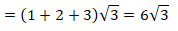
b) 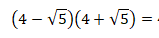
Aplcando a propriedade distributiva, temos:
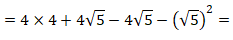
Simplificando as expressões simétricas, temos:
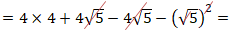
Posterimente, resolve-se as operações presentes no exercicio. Sendo assim, temos:
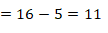
3.Resolução dos exercícios sobre Intervalos de números reais
Representando os conjuntos em forma de intervalo, temos:
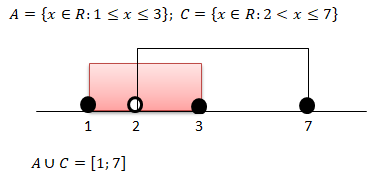
Representação do Conjunto A:
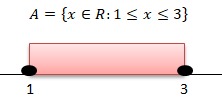
Conjunto B:
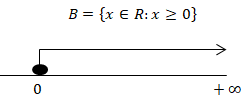
Conjunto C:
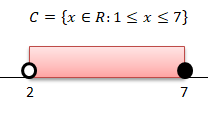
Calculando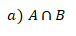
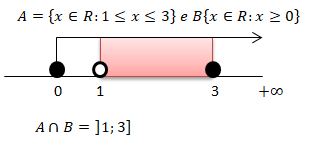
Calculando 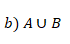
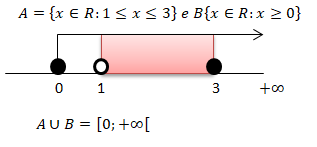
Calculando 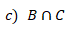
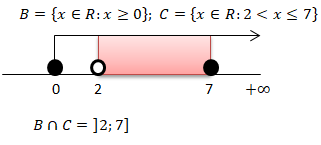
Calculando 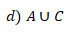
4.Resolução do exercício sobre sistema de duas equações
- 2x-4y=6
- x+y=6
Resolsovendo o sistema, aplicando o medo de redução, temos:
- 2x-4y=6…………….2x-4y=6
- x+y=6/.(4)………….4x+4y=24
Simplificando os termos em y, temos:
- 2x-4y=6
- 4x+4y=24
……………………….
2x+4x=6+24
6x=30/:(6)
x=5
Substituindo x=5, na 2ª equação, temos:
x+y=6
5+y=6
y=6-5
y=1
C.s:(5;1)
5. Resolução dos Problemas que envolvem sistemas de duas equações a duas incognitas
- Um agricultor tem 240 galinhas em duas capoeiras, numa das capoeiras tem o dobro de galinhas que na outra. Quantas galinhas tem em cada copeira? ( Método a sua escolha)
1ª capoeira…..x
2ª capoeira…..y
<< Tem 240 galinhas em duas capoeiras>>
x+y=240
<< Numa das capoeiras tem o dobro de galinhas que na outra>>
x=2y
Formando o sistema de equações, temos:
- x+y=240
- x=2y
Resolvendo o sistema, aplicando o método de substituição. Vamos substituir a 2ª equação(x=2y) na 1ª equação. Assim ,temos:
1ª equação: x+y=240
2y+y=240
3y=240/:(240)
y=80
Substituindo y=80, na 2ª equação , temos:
x=2y
x=2.80
x=160
Solução( 160; 80)
Portanto, numa capoeira tinha 160 galinhas e na outra 80 galinhas.
6.Resolução do exercício sobre equações do 2º grau
x2-2x-8=0
Resolvendo a equação do 2º grau, aplicando a formula resolvente/ Bhaskara, temos:
a=1; b=-2; c=-8
Substituindo na formula resolvente, temos:
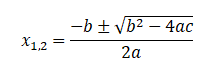
Substituindo os valores da a , b e c na formula resolvente, temos:
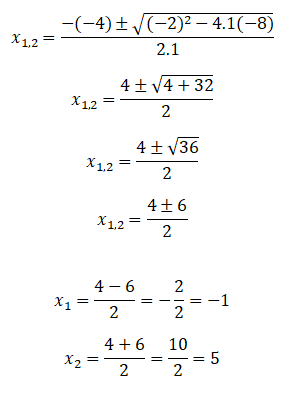
x1=-1 e x2=5
7. Resolução do exercícios sobre Inequação do 1º grau
6k-4(k-6)<30
Simplificando os parentese, temos:
6k-4k+24<30
Agrupando os termos semelhantes, temos:
2k<30-24
2k<6/:(2)
k<3
C.S=]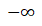
Leia também:



Foi muito útil e totalmente elucidativo.
Muito obrigado pelo feedback!!